导语：失踪的正方形谜题属于数学中的一种视错觉，它描述的是4个几何图形的2种不同拼法，都是13乘5的大三角形，但是第二种方法却缺少了一个1乘1的正方形，其中的下面就跟着探秘志小编一起来看看吧!

失踪的正方形是什么?

失踪的正方形实际上就是数学中的一种几何视觉错觉，这是在1953年由一个纽约的业余魔术师保罗嘉理发明的，不过这样的裁剪原理在1860年就被数学界所知，失踪的正方形其实就是2种几何拼接方法，拼完的每一个图形都是13乘5的三角形，但是只有其中的一种方法少了一个1乘1的正方形。

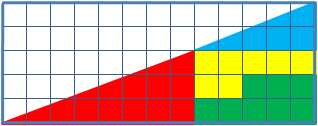
在拼接的过程中并没有对图形动手脚，只是将原本的三角形分成了四个特定的图形，然后再重新拼接，可是新的三角形却少了一块，这让很多人疑惑不解，到底是哪儿丢失了这一个正方形的面积呢?

失踪的正方形去哪儿了?

其实第二种拼法拼成的三角形，并不是真正的三角形，红色部分和蓝色部分的倾斜度有轻微的差异，所以这时候的“三角形”就会多出一条十分细小的平行四边形的边，这就是那块失踪的正方形多出来的面积，如果将两张图重合，就会明显的发现，而这个细长的平行四边形就恰好占据了一格的面积。

所以对于没有精确运算，只是凭借肉眼观察的人眼来说，这样细微的差别根本无法看到，所以就会显得这个失踪的正方形很突兀，好像十分不合情理，这就像晃动的方块幻觉一样，所以我们就用算法来精确的证实一下吧!

根据图上的格子来看，四个图形占了32个单位，但是总三角形是13乘5的，所以通过计算得出了32.5个单位，这一下就多了0.5个单位，因为蓝色三角形的长宽比是5:2，而红色是8:3，明显不是一个长宽比，所以斜边实际上缩短了。

而总共缩短的长度是一个单位的1/28，这一点细微的溢出，在人眼看来并不明显，所以当这个溢出的平行四边形合拢时，就是刚好一格的大小，也就正好是失踪的正方形。

结语：在数学上还有很多有趣的现象，比如毕达哥拉斯树，就是利用勾股定理所画出的一棵树，所以说数学其实也可以很有意思。

导语：不可能图形是一种只能在二维世界存在的图形，属于一种典型的视错觉现象，是由于人类视觉对二维图形的三维投影出现了光学错觉导致的，不可能图形在三维世界中是不可能存在的，下面就跟着探秘志小编一起来看看不可能图形吧!

不可能图形是什么?

不可能图形其实就是一种视错觉，是人类视觉对一个二维图形的三维投射，都不可能在三维空间中存在，就像纪念碑谷中的那些诡异的图形链接，实际上都是视觉系统的错误判断，就像艾宾浩斯错觉一样，这样的图形其实还有很多，比如无尽阶梯，彭罗斯三角形等。

不可能图形的最先提出者是莫里茨·科内利斯·埃舍尔，他是著名的视错觉画家，他的画作中大部分都是此类不可能图形，这位荷兰籍的画家就是以画面中的数学性而闻名的，所以经常能在他的画中看到许多的数学概念，比如对称，分形和双曲几何等。

无尽的阶梯

无尽的阶梯又被称为彭罗斯阶梯，这是一个十分著名的几何悖论，描述的就是一个始终走不到头的台阶，可以无限的循环，就像彭罗斯三角形一样。这是1985年英国数学家彭罗斯提出的，这是高维空间才能实现的图形，所以不可能在三维空间中存在，就像克莱因瓶一样。

彭罗斯三角形

彭罗斯三角也是不可能图形中的一个，也是最纯粹的不可能图形，同样是由英国数学家彭罗斯设计并推广的，发表于1958年2月的《英国心理学期刊》上。整体看起来像是一个三角立体图形，但是仔细观察会发现，这个图形无法在三维中实现。

埃舍尔作品：不可能的世界

《瀑布》就是不可能的世界中的其中一个，一条瀑布从高处倾泻而下，转动着水轮，但是顺着水流慢慢向前，你却会发现水流竟然留到了瀑布的上方，之后又向下流去，这样周而复始，循环往复，形成一个既矛盾又有趣的画面。

《观景楼》也是不可能世界中的一个，整栋楼看似正常的排列，但是仔细观察就会发现，其中一个竖立的梯子它的最上面靠在观景楼的外边，但是最下面却伸进了观景楼的里面。

《画手》相信很多人都看过，一只手画着另一只手，让人分不成到底哪个才是真正的画。所有的一切仿佛都被固定在画中，但是又好像没有固定。

结语：不可能世界中还有很多不可能图形的体现，埃舍尔就是用这种独一无二的画法，让人印象深刻，空间的错乱让人不禁感叹数学的艺术美。