导语：雪作为一种大自然现象，其在冬季十分常见。雪作为一种固体水，有些地方冬季会下雪，有些地方全年甚至几年都不会下雪，那么你们知道雪形成的原因是什么吗?以及下雪要具备什么条件吗?下面呢就由探秘志小编为大家一一揭晓，感兴趣的不妨一起往下看!

雪形成的原因是什么?

雪是大气中形成一种冰晶，它落在地球表面时发生了许多变化。谈到雪时，重要的是要记住，雪与水密切相关，即从液态到固态，最后又回到蒸汽中。

雪是在天气气温冷到一定程度才会形成的，在寒冷天气较长的地区，如两年或更长的时间，冰川可能会形成，但在少数地方会发生这种情况。对大多数地方来说，随着夏天的临近，雪会融化。然后，这些冰水被蒸发回大气中，继续循环进行。

下雪要具备什么条件?

雪的形成必须满足几个条件。首先，大气温度必须足够低。与普遍的看法相反，温度不需要低于零度才能形成雪，所需温度在2⁰以下。

因为雪是由大气中的水蒸气构成的，所以它有一个简单的逻辑，即水汽应该存在。最后，冰晶必须碰撞，从而形成更大的冰晶，称为雪花。最后一项要求的原因相当简单，要想形成雪，冰晶必须落在地上。然而，它们本身并不重，不足以被重力所牵引。

湿雪和干雪的区别

这两个术语可能有误导性，雪是固体状态下的水，所以当雪被定义为干”或“湿”时，它可能听起来会很混乱。如果有水，雪被定义为潮湿。在雪形成的条件下，“干”和“湿”不仅仅是字面意思。相反，它们是用来区分每种类型的雪是如何形成的，以及由此产生的雪的类型的属性。

当雪花在大气中形成时，重力就会取代。如果雪花在干燥的空气中落下，那么雪花的外部部分就会干燥。因此，雪颗粒之间的粘合能力会减弱。

由此产生的雪将变得不那么紧凑和轻，事实上，它将足够轻，可以被风吹走。这种雪非常适合冰上运动，被称为“干”雪。

如果气温略高于0⁰，那么落在空气中的雪花就会慢慢融化，雪花使水颗粒之间有更多的凝聚力。由此产生的雪花更大，但也更紧凑。这种雪可以作为一些乐趣活动，如制作一个雪人，因为它的紧凑，这种类型的雪被描述为湿的。

雪对作物的影响

雪可以保护农作物不被冻伤，其可以起到保温效果，受雪保护的庄稼可以放心过冬。雪还可以缓解一些地方的干旱情况，给来年的庄稼播种和壮苗打好基础。雪还可以为农作物储备水分，增强土壤肥力。

雪对人的影响

如果经常用雪水洗澡的话，不仅能够减少人体疾病，还能增强身体抵抗力，促进血液循环。如果有条件的话，长期饮用干净的雪水，有利于延长寿命，一些居住在深山老林中的人都是这样做的，这也是他们长寿的原因之一。

为什么雪水有这么神奇的功效呢?其实是因为雪水所含的重水要比普通水数量少1/4，有人曾经做过实验，重水能够抑制生物的生命过程。不过，鱼类在重水中会立即死亡。

对于农村人来说，下雪给田里庄稼松土和增加水分，为大丰收做准备。对城里人来说，下雪增添了乐趣，改善了空气质量。

导语：世界上很多事情并不是非黑即白的，有很多东西不能细推，推敲出来就会出现矛盾，也就是大家常说的悖论。有关悖论的问题还有很多，有些人也疑惑龟兔赛跑是悖论吗，还有神奇的费米悖论等等，下面探秘志小编为大家介绍另外一种神奇的悖论-生日悖论，下面一起了解一下吧。

生日悖论

这个就是指一个房间里有23个或23个以上的人，那么至少有两个人的生日相同的概率要大于50%。也就意味着一个30人的小学班级中，两人生日一致的可能性更高。假如人数是30的几倍的话，这个概率更是会大于99%。

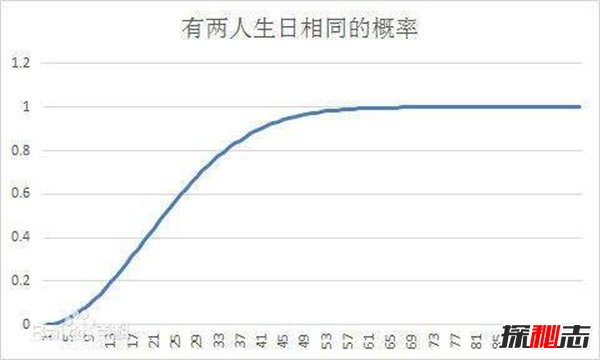
虽然从引起逻辑矛盾方面来看，似乎这个并不算是一种悖论，只有从这个数学事实与一般直觉相抵触的意义上，它才称得上是一个悖论。

悖论内容

如果一个房间里有23个或23个以上的人，那么至少有两个人的生日相同的概率要大于50%。这就意味着在一个典型的标准小学班级(30人)中，存在两人生日相同的可能性更高。对于60或者更多的人，这种概率要大于99%。

不计特殊的年月，如闰二月。

先计算房间里所有人的生日都不相同的概率，那么

第一个人的生日是 365选365

第二个人的生日是 365选364

第三个人的生日是 365选363

:

:

:

第n个人的生日是 365选365-(n-1)

所以所有人生日都不相同的概率是：

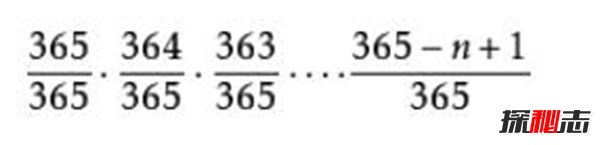
那么，n个人中有至少两个人生日相同的概率就是：

所以当n=23的时候，概率为0.507

当n=100的时候，概率为0.999999692751072

对于已经确定的个人，生日不同的概率会发生变化。下面用随机变量计算：

令X[i,j]表示第i个人和第j个人生日不同的概率，则易知任意X[i,j]=364/365

令事件A表示n个人的生日都不相同

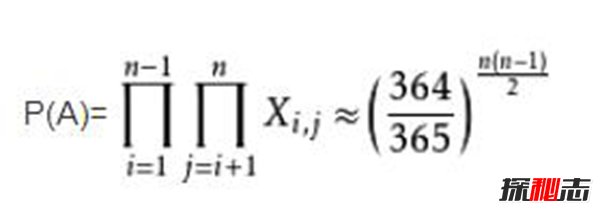
解P(A)<1/2，由对数可得：n>=23

相比之下，随机变量也同样的简单易懂而且计算起来要方便得多

理解悖论

这个问题的关键在于认识到相同生日的搭配可以是相当多的。比如23个人可以产生23 × 22/2 = 253种不同的搭配，而这每一种搭配都有成功相等的可能。从这样的角度看，在253种搭配中产生一对成功的配对也并不是那样的不可思议。

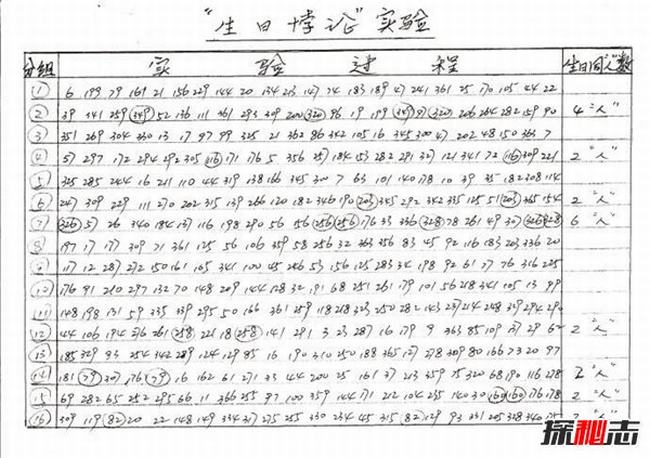
换一个角度，如果你进入了一个有着22个人的房间，房间里的人中会和你有相同生日的概率便不是50%了，而是变得非常低。原因是这时候只能产生22种不同的搭配。生日问题实际上是在问任何23个人中会有两人生日相同的概率是多少。

结语：看了这个生日悖论问题，大家是不是觉得和世界十大著名悖论一样也相当有意思。有些人认为这个悖论不能应用在生活中，实际上并不是这样，生活中很多东西都运用了这个有关悖论。