导语：数学是现在一门十分重要的学科，影响了生活的很多方面。但是数学的发展并全是一帆风顺的，在数学史上也爆发过三次比较严重的危机，下面探秘志小编带大家一起了解一下吧。

第一次数学危机

发生时间是公元前500年左右，和精准度有一定的关系。我们平时需要用到的数学知识，只需要精准到一定的程度就可以了。当时古希腊毕达哥拉斯学派认为，世界上所有的数字都可以用[db:tags]/b的形式表示，需要注意的是a、b都是整数。这些数字被称为有理数。但是后来希帕索斯突然发现了一些事情，假设有一个等腰直角三角形，直边都为1，斜边则是(√2)，并不满足这个条件，后来这些气急败坏的学者们不愿意承认这个事实，就把希帕索斯扔到海里去了。

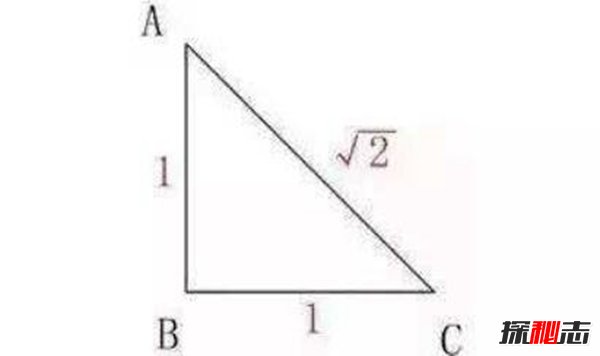
不过虽然希帕索斯死了，但是又有更多的学者发现了√2，√3，√5等等。这次数学危机导致纯代数的地位直线下降，而几何学的地位则上升了很多。并且还形成了欧几里得《原本》的公理体系与亚里士多德的逻辑体系，这次数学危机让东西方数学走上了不同的道路。

第二次数学危机

这次危机的发生时间在十七八世纪，主要参与的数学家是牛顿和莱布尼兹，他们和教会的贝克莱大主教是敌对关系。危机的核心问题在于微分中有关无穷小的定义，不管是牛顿还是莱布尼兹对于无穷小的定义都比较粗糙，这和讲究严谨的数学是不相符的。因此遭遇了强烈的抵抗和抨击。

后来柯西用了极限的方法来重新定义了无穷小量，这让微积分更加全面和发展，这也让数学增加了更多的活力。

第三次数学危机

第三次危机的发生时间在十九世纪下半部分，主要对抗的人物是群论(集合论)的创立者康托尔和数学家罗素。当时康托尔创立了著名的集合论，这在一段时间内引发人们的讨论，一部分人对其十分赞扬另外一部分则强烈的攻击。不过在不久之后基本上所有的数学家都接受了，并且发现集合论的强大之处。

但是当集合论的讨论越来越多，在数学界的影响越来越大时，人们发现了一个有关的悖论，那就是有名的罗素悖论。

罗素悖论：S由一切不是自身元素的集合所组成，那S包含S吗?用通俗一点的话来说，小明有一天说：“我正在撒谎!”问小明到底撒谎还是说实话。罗素悖论的可怕在于，它不像最大序数悖论或最大基数悖论那样涉及集合高深知识，它很简单，却可以轻松摧毁集合理论。

当这一悖论提出后，各大数学家都开始提出自己的设想，人们希望通过某些方法对康托尔的集合论进行改造，并且设立新的原则来排除悖论。后1908年策梅罗在自己这一原则基础上提出第一个公理化集合论体系，在被其他数学家改进之后被称为ZF系统，这在很大的程度上弥补了集合论缺陷。

结语：三次重大的数学危机都在一定程度上推动的数学的发展和进步，让其根基更加牢固，应该也算是一件好事吧。

导语：说到数学史上三大重要危机，大家应该都有所耳闻。但是说到第四次可能很多人都摸不着头脑，实际上第四次危机爆发时间至今已经20多年了，不过当时因为网络不发达的缘故，所以不为人所知，下面探秘志小编带大家深刻了解一下。

数学史上的第四次危机

第四次数学危机准确来说是数论，主要是说数论的研究对象不仅仅是数。假如有一门学科分别研究：人、树、花，那么这门学科叫花学，相应理论称为花论，实际上这并不合理，主要讨论的还是第三次数学危机，有关集合论的相关问题。

集合的类名用集合中的元素命名实际上并不十分合理，虽然强行命名没有太大的关系，但是有些地方还是比较奇怪。

无限循环小数悖论

无限循环小数是小学数学中的一些知识，在很多时候会出现除不尽的情况，比如

1&pide;9 = 0.111111…(数字1无限循环)

1&pide;3 = 0.333333…(数字3无限循环)

1&pide;1.3 = 0.769230769230769230…(数字串769230无限循环)

无限循环小数具有特殊的性质：

(1)它的循环体至少有一位数字;

(2)它没有最后一位，永远写不到头。

无限循环小数0.999…更是奇怪。现有的数学体系既能证明它等于1，又能证明它不等于1。

我们首先证明无限循环小数0.999…等于1。

数学课本上写着：无限循环小数可以转化为分数

0.111… = 1/9 (1)

两边同时乘以9，得

0.999… = 9/9 (2)

故有

0.999… = 1 (3)

证毕。

现在，我们再证明无限循环小数 0.999… 不等于1。

设 n 是无限循环小数0.999…中9的个数，根据数学归纳法

n = 1时，0.9 ≠ 1成立;

n = 2时，0.99 ≠ 1成立;

n = 3时，0.999 ≠ 1成立;

……

n = ∞时，0.999… ≠ 1成立;

于是

0.999… ≠ 1 (4)

证毕。

这两种办法都是现在数学中比较严谨的证明方法，但是得出的结论却截然不同，互相矛盾，这一悖论被称为“无限循环小数悖论”。这一悖论的出现严重影响了当代数学，并且带来了比较严重的危机，甚至给摧毁当代数学体系。

结语：在人类数学的发展中，一共出现了三次比较严重的危机，每一次都为数学带来了更多的发展，可以预见经过这次悖论，数学将更加发展进步。